EXAMEN DE DINAMICA

ARBOL DE DECISIONES - EPPEN GOULD

El análisis de decisión brinda información sobre las diferencias entre las alternativas definidas, y genera sugerencias de nuevas y mejores alternativas. Usamos números para cuantificar valores e incertidumbres subjetivos, lo cual nos permite comprender la situación de decisión. Los resultados numéricos deben reconvertirse para generar información cualitativa.

Toda decisión necesita un decisor responsable. El decisor tiene varias alternativas, y debe elegir una. El objetivo del decisor es elegir la mejor alternativa. Después de que se ha tomado una decisión,, pueden producirse eventos sobre los que el decisor no tiene control. Cada combinación de alternativas elegida, seguida por un evento, conduce a un resultado con algún valor mesurable. Los gerentes toman decisiones en situaciones complejas. Las matrices de árbol de decisiones y pago describen estas situaciones y añaden estructura a los problemas.

Elementos de los modelos de análisis de decisión

·         Hay un decisor responsable individual. Por ejemplo, el CEO de una compañía que quizás deba rendir cuentas ante los accionistas.

·         Un número finito de eventos (futuros) posibles, llamados Estados de la Naturaleza, es decir un conjunto de escenarios posibles. Los estados de la naturaleza se identifican y agrupan en el conjunto S; los miembros se denotan como s. el conjunto S es un grupo de conjuntos mutuamente excluyentes. Es decir, solo puede ocurrir un estado de la naturaleza. ¿Qué puede hacer la naturaleza?

·         Un conjunto finito de alternativas posibles de decisión. Hay una acción a, miembro del conjunto A, que puede ser adoptada por el decisor. Solo puede adoptar una. ¿Qué puedo hacer? Una buena decisión requiere buscar un conjunto más rico de alternativas que las que se presentaron inicialmente o que las aceptadas TRADICIONALMENTE. Sea breve en la parte de la lógica y la razón de su decisión. Es probable que existan mil cosas en un automóvil, pero usted no las necesita todas para tomar la decisión. Con media docena es suficiente.

·         La manera más sencilla de formular el problema de decisión es usando una matriz de beneficios (tabla). Hay una matriz de beneficios X bien definida, monetaria (y luego de utilidad) sobre dos conjuntos de dominio dimensionales A y S. las filas y las columnas se asignan a las alternativas de decisión posibles y a los estados posibles de la naturaleza, respectivamente. Normalmente no es tarea sencilla construir esta matriz; por lo tanto puede requerir algo de práctica.

Fuentes de error en la toma de decisiones

La fuente principal de errores en los problemas de toma de decisiones arriesgadas son las presunciones falsas, no tener una estimación exacta de las probabilidades, depender de la expectativa, dificultades en medir la función de utilidad, y los errores de pronóstico.

Existen tipos diferentes de modelos de decisión que ayudan a analizar distintos escenarios dependiendo de la cantidad y el grado de conocimiento que tengamos. Los tres tipos más ampliamente utilizados son:

1.     Decisión tomada con pura incertidumbre,

2.    Decisión tomada con riesgo,

3.    Decisión tomada comprando información (empujando el problema hacia el  “polo” determinista)

En las decisiones tomadas con pura incertidumbre, el decisor no tiene ningún  conocimiento, ni siquiera de la probabilidad de ocurrencia de cualquier estado de la naturaleza. En estas situaciones, el comportamiento del decisor se basa puramente en su actitud hacia la incógnita. Algunos de estos comportamientos son los optimistas, los pesimistas y los de arrepentimiento entre otros.

o   Optimista: El vaso esta medio lleno

o   Pesimista: El vaso esta medio vacio

o   Gerente: El vaso es el doble de la grande de lo necesario.

La persona pública (es decir el gerente) tiene que tener cierto conocimiento de los estados naturales, para poder predecir las probabilidades de cada estado. De lo contraio no podrá tomar una buena decisión que sea razonable y defendible.

Comportamiento según los tipos de personalidad y la toma de decisiones con pura incertidumbre

·         Pesimismo, o Conservador (maxi min). Hipótesis de mínima. Las cosas malas siempre me suceden a mí.

·         Optimista, Agresivo (maximax). Las cosas buenas siempre me suceden a mí.

·         Coeficiente de Optimismo (índice de Hurwicz). A mitad de camino: Ni demasiado optimista ni demasiado pesimista.

·         Mínimo arrepentimiento: (Perdida de Oportunidad de Savage). Odio las lamentaciones. Debo minimizar las situaciones deplorables. Mi decisión debe ser tal que válgala pena repetirla. Solo debería hacer las cosas que siento que podría repetir con placer. Este es, posiblemente, el mejor criterio a aplicar en las situaciones donde debe tomarse una decisión que puede generar problema u oportunidades.

·         El arrepentimiento es el beneficio o el rédito de la que hubiera sido la mejor decisión, dadas las circunstancias, menos el beneficio de la decisión tomada concretamente, dadas las circunstancias.

CERTEZA, RIESGO E INCERTIDUMBRE

CERTEZA:

• EL 15 DE NOVIEMBRE ES MI CUMPLEAÑOS
• LOS MIÉRCOLES TIENES CLASES DE INVOPE II
• TU MAMA TIENE 45 AÑOS
• LA TERCERA SEMANA DE JUNIO ES EL DÍA DEL PADRE
• EL 28 DE JULIO TENEMOS NUEVO PRESIDENTE OFICIALMENTE

RIESGO:

• GANARE ESTA NOCHE EN EL BINGO
• ME DIRÁ LA FLAQUITA QUE SI DESPUÉS DE LA DECLARACIÓN (AMIGA)
• SERA HOMBRE O MUJER EL BEBE QUE ESPERO
• NACERÁ EN AGOSTO O JULIO
• ESTA NOCHE BAILARE O SOLO TOMARE

INCERTIDUMBRE

• LLEGARE VIVO A MI CASA
• YANINA ME ENSEÑARA INVOPE II
• GOBERNARA BIEN OLLANTA LOS PRÓXIMOS 5 AÑOS
• DICSON SE CASARA ALGÚN DÍA
• TU...!!!!! O.O!! EL QUE LEES TE PONDRÁS FALDA ALGÚN DÍA

PROBLEMA 4 - PROGRAMACIÓN DINAMICA

Un sistema eléctrico consta de tres componentes, los componentes funcionan independientemente unos de los otros. Se tiene un presupuesto de $1000, y el componente 1 cuesta $200/unidad, el componente 2 cuesta $200/unidad y el componente 3 cuesta $300/unidad. ¿Cuántas unidades de cada componente se debe comprar para maximizar la probabilidad de funcionamiento?

Solución:

PROGRAMACIÓN DINÁMICA - PRODUCCIÓN

PROBLEMA 1.
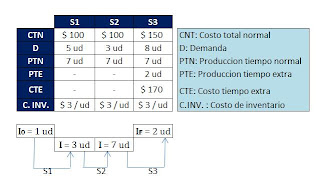
Considere el problema de programación de la producción de un producto las 3 semanas siguientes. El costo unitario de producción es de $100 para las 2 primeras semanas y $150 para las dos últimas. Las demás semanales son 5,3 y 8 unidades respectivamente y tienen que ser satisfechas. Las plantas pueden producir un máximo de 7 semanales. Además, se pueden emplear horas extras durante 2 últimas semanas, esto incrementa la producción en 2 unidades por semana, pero el costo de producción sube en $20 por unidad extra. El exceso de producción se puede almacenar a un costo unitario de $3 por semana. Si al inicio se tiene 1 unidad de inventario y se desea tener al final 2 unidades ¿Cual debe ser el plan de producción?

solución :

PROGRAMACIÓN DINÁMICA - RICHARD ERNEST BELLMAN

BIOGRAFIA Y APORTES

Richard Ernest Bellman (1920–1984)

·         Fue un matemático aplicado, cuya mayor contribución fue la metodología denominada programación dinámica.

·         Bellman estudió matemáticas en la Universidad de Brooklyn, donde obtuvo una diplomatura.

·         Luego en la Universidad de Wisconsin, donde obtuvo su licenciatura.

·         Posteriormente comenzó a trabajar en el Laboratorio Nacional Los Álamos en el campo de la física teórica.

·         En 1946 obtuvo su doctorado en la Universidad de Princeton.

·         También ejerció la docencia en la universidad del sur de California(EE. UU.), fue socio de la Academia Americana de las Artes y las Ciencias (1975) y de la Academia Nacional Americana de Ingeniería (1977).

·         En 1979 el IEEE le otorgó la medalla de honor por su contribución a la teoría de los sistemas de control y de los procesos de decisión, en especial por su contribución con la programación dinámica y por la ecuación de Bellman.

·         Su primer estudiante de doctorado fue Austin Esogbue, que es actualmente profesor en el Instituto tecnológico de Georgia, en el departamento de ingeniería industrial y de sistemas.

PROBLEMA PROGRAMACIÓN DINÁMICA DETERMINISTICA

PROBLEMA 1

Cierto estudiante desea destinar los siete días de la semana próxima a estudiar cuatro cursos. Necesita al menos un día para cada curso y el puntaje que puede lograrse da en la siguiente tabla:

Días de estudio	Curso 1	Curso 2	Curso 3	Curso 4
1	13	15	12	16
2	15	15	12	16
3	16	16	17	19
4	17	19	18	19

¿Cuántos días debe estudiar cada curso para lograr un puntaje?

Solución 

LUEGO SE HACE EL RECORRIDO 

PROGRAMACIÓN DINÁMICA - PROBLEMA RUTA CORTA

PROBLEMAS DE PLE

1.       Escribo cartas cuando estoy enamorado, y no escribo cuando estudio.

Y1+Y2<=1

2.       Si no tomo desayuno entonces hago deporte y paseo al perro

Y1+ Y2>=1      1+y3>=1

3.       Matilde ingresara si practica en casa y se prepara en KEPLER

Y1+Y2>=2

4.       Si el profesor no me castiga entonces terminare mi tarea.

Y1<=Y2

5.       Gerardo no juega básquet sin embargo juega futbol

Y1+Y2<=1

6.       El Perú es es un país americano porque es un país europeo solo si no es americano.

Y1+Y2<=1

7.       Dionisio estudia o trabaja pero si no estudia entonces trabaja.

Y1+Y2<=1

8.       Manuel  se dedica a hacer taxi, cuidar los niños o  las tareas del hogar en las mañanas.

Y1+Y2+Y3<=1

9.       Si salgo el fin de semana también saldrán mis amigos

Y1=Y2

10.   Si se tiene manzana, pera, uva, plátano y naranja solo tengo para comprar una fruta ocmo máximo.

Y1+Y2+Y3+Y4+Y5<=1